Shake one end of a
spring or rope that is tied firmly to a wall or other
unmovable support to produce a train of waves that moves down
the spring, reflects from the end, and travels back in the opposite
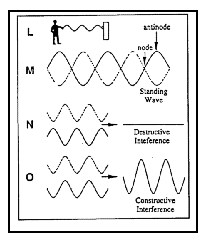
direction (Figure L). If you shake the rope in such a manner
that
wavelength, amplitude, and frequency remain constant, the incident
and reflected waves will interact to form a standing wave as
shown in Figure M. A standing wave results when two identical
waves move through the same medium in opposite directions. It
is known as a "standing" wave because it does not move
even though its component waves do.
The points where no movement of the rope occurs are called nodes. The locations where super-roughs and super-crests successively appear are known as antinodes. A standing wave is formed because the waves moving in opposite directions interfere with each other, as shown in Figure N and O. When a crest of one wave overlaps the trough of another, destructive interference occurs and the waves cancel (Figure N). Though the energy-carrying waves are simultaneously passing the same point, there is no visible response of the spring (medium) at that point. When the crest of one wave overlaps the crest of another or the trough of one wave overlaps the trough of another, constructive interference occurs and the waves add (Figure O).
Part 1. Standing waves in a rope or coiled spring:
Firmly attach one end
of the spring or rope to a solid support and shake it up and
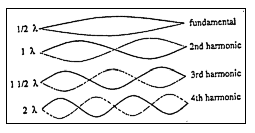
down, adjusting the frequency to produce a standing wave of _
wavelength as shown in Figure P. This is the natural frequency
for this length of spring and is also referred to as the fundamental
frequency. The fundamental frequency is the lowest possible frequency
for the formation of standing waves. Shake the spring or rope
with twice the frequency to set up a standing wave of 1
wavelength (Figure Q). Shake even faster to set up a wave of
1_ and 2 wavelengths (Figure R and S). The wave patterns in Figures
!, R, and S are referred to as the second, third, and fourth
harmonics respectively. Does it require more of your energy to
establish
the fourth harmonic than the second harmonic? Why or why not?
What is the relationship between frequency and energy?
Part 2. Standing waves on the surface of a liquid:
Place a clear rectangular
tray on an overhead projector and fill with water to a depth
of about 1.0 to 1.5 centimeters. Place a board in
the pan and move it back and forth at a constant frequency and
observe the wave patterns on the screen. Establish the fundamental
frequency by adjusting the frequency of the board so that the
oscillations just match the round-trip time of a reflected wave.
Be patient, since it may take some practice to establish clear
standing wave patterns. If you have a wave-generating machine
adjust its
frequency to establish the second, third, and fourth harmonics.
Part 3. Interference of waves on the surface of a liquid:
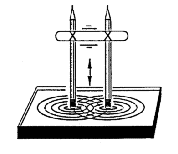
Fasten two pencils together as shown in Figure T and repeatedly touch the surface of the water at a constant frequency and observe the interference pattern caused by the waves. Observe the effect of changing the frequency of tapping the water with the pencils.