P201 Menu
Exploratories
Gravitational
and Electric Potential Energy
PART A.
Problem:
What is meant by Electric Potential,
Electric Potential Energy and Change in
Electric Potential Energy?
Introduction:
Definition of Potential
#1 (from Webster's Ideal Dictionary): Something that can
develop or become actual
Many times when a coach of a
sport is interviewed on television, if the interview is before
the season starts, he or she indicates that the team has "potential".
They usually do not say that their teams are "Weak, Slow
and Chicken" ! What does it mean when a coach says, "the
team has potential? "
Gravitational Potential Energy
Early in the course you probably
discussed the acceleration of gravity, the force of gravity and
Newton's Law of Universal Gravitation. Later in this course,
you probably studied potential energy.
Procedure #1:
You have a text book. Hold this
book in this room (up off the table or desk). Assuming the gravitational
potential energy at the level of the floor of this room is zero,
what is the gravitational potential energy of your book? Express
your answer in joules.
Change in Gravitational Potential Energy
Procedure #2:
Assume that the level of the
floor in this room has gravitational potential energy of zero
joules. Place your textbook on one of the chairs in the room.
Calculate its gravitational potential energy in joules. Now move
the book horizontally to a similar chair elsewhere in the room.
Did you do work "on the book"? Explain your answer.
(Review the definition of work, if needed.)
Now move the book from the chair to a laboratory table in the
room. With the book lying on the table, calculate the book's
gravitational potential energy. Was there a change in gravitational
potential energy? If so, what was the change in gravitational
potential energy? Express your answer in joules.
Was work done "on the book"
in moving it from the chair to the table? Explain your answer.
Gravitational Potential Difference
In the previous activity, you
have used the fact that the change in gravitational potential
energy is equal to the mass of the object multiplied by the acceleration
due to the earth's gravitational field multiplied by the change
in the height of the object. ( DPE = mgDh) If we were to divide both side s of
the equation by the mass, then DPE/m =gDh. This is called the difference in gravitational
potential or the gravitational potential
difference.
At the surface of the
earth there is a gravitational potential difference of about
9.8 joules/kilogram for every one meter increase in elevation.
Potential difference describes how much the potential energy
changes if a unit test object is moved from one point to another
in a force field. The object does not have to move for
the potential difference to exist. The potential difference is
created by the source that is producing the force field, not
by the test object.
A) A potential exists at any
point as a result of a field. A gravitational potential (gh)
exists at any point in the space associated with a gravitational
field. Similarly, an electrical potential (Ed) exists at any
point in the space associated with an electric field.
B) If we place "our"
charge 'q' in an electric field it will have an
electric potential energy (PE = Fd = qEd). This is analogous
to
gravitational potential energy (PE=Fd=mgh).
C) The effect of moving a mass
in a gravitational field creates a change in potential energy
of "our" mass 'm' such that DPE=mgDh. When work is done in moving our charge
'q' in the electric field, there is a change in the electric
potential energy such that DPE = qEDd. If we find the change in the electric
potential energy for each unit of "our" electric charge,
then DPE
/ q = EDd.
D) This change in electric potential
energy/charge is measured in units of volts ( 1 volt = 1 joule
/ 1 coulomb)
Notice that this quantity is
also the change (or difference) in electric potential (E Dd) sometimes
called the electric potential difference.
E) A battery functions by creating
a difference in electric potential
energy between two points. Definition of Potential # 2 (from
Webster's Ideal Dictionary): the degree of electrification with
reference to a standard
PART B.
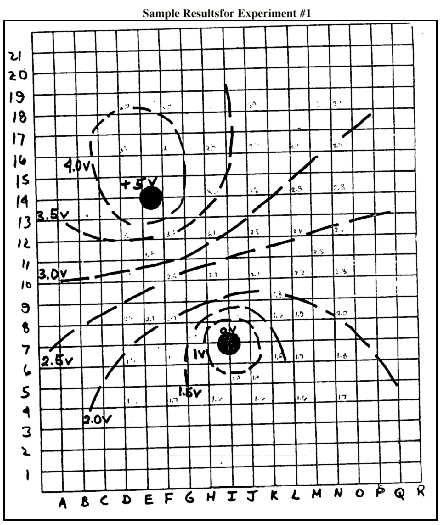
Experiment #1 -
Problem:
How can electric potential differences
be detected?
Materials:
Pyrex baking pan or clear plastic
tray, voltmeter, connecting wires with alligator
clips, two electrical conductors that sink in water, power supply,
graph paper and salt.
Procedure:
1. Place the graph paper on a
table and center the baking dish on the grid. Hook one alligator
lead to the positive terminal and another wire to the negative
terminal of the supply. Attach each of the wire ends to one of
the conductors, and separate the conductors in the dish.
2. Fill the dish one forth full
with water.
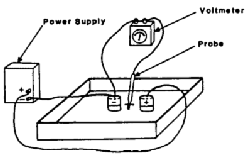
3. Connect the power supply to
the electrodes as illustrated and adjust the
potential to approximately 10 volts. Attach one lead of the voltmeter
to one of
the electrodes and let the other lead of the voltmeter be the
"probe" that will be
used to plot the equipotentials. As a preliminary check, place
the probe on the "+" electrode and not the full scale
reading. then move the probe into the salt water very near the
"+" electrode. You should note only a small change
int he reading in the voltmeter. If a large change is observed,
this means either the water is not sufficiently conductive or
you should use a voltmeter with a higher internal
resistance. Now move the probe between the electrodes and you
should observe a
fairly linear change in voltage with distance for the "-"
electrode. You are now
ready to plot equipotentials.
4. Draw the locations of the
conductors on the graph paper an d label them with the voltage
readings of your voltmeter.
5. With your positive voltme
ter probe in the water, note the voltage reading. Move the probe
in the water, keeping the voltage reading at the same value.
How far does this path go? Sketch this pattern on your graph
paper and label the line with the voltage you chose.
6. Choose other voltage values
and similarly sketch their patterns on the graph paper until
you mapped out the area between and around the conductors.
7. With another color pen or
pencil draw a point any place on your map to
represent a moveable positive charge. Predict the path it would
take by
drawing a line with your colored pen or pencil.
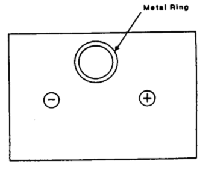
8. Now place a large metal ring
in the tank between the electrodes. You will
notice that the potential will change as you move the probe in
the region
outside of the ring but that it will remain the same when the
probe is
moved around in the region inside of the metal ring. Hence a
conductor placed in
an electric field will have the same potential everywhere.
Summing Up:
1. What generalizations ca n
you make from this exploration?
2. Where would a positive test
charge have the least potential energy?
3. How much energy must be added
to the system to move 1 electron, 1 meter in a direction along
one of the equal potential lines.
4. If lightning strikes a tree
20 meters away, would it be better to stand facing the
tree, your back to the tree, or your side to the tree? Assume
your feet are a
comfortable shoulder width apart. Explain your answer.
Summing Up (Comments):
1. Students' generalizations
will vary. They may recognize that equal potential lines
are more concentrated near surfaces that have a smaller radius
of curvature. Some
students may recognize that the force on a charge will be at
right angles to the
equal potential lines, but don't push this point until after
the students have made
their generalizations. This activity should be most appropriate
to build the concept
of an electric field.
2. A positive test charge would
have the least potential energy next to the conductor
established at 0 volts.
3. If an electron is moved any
distance along the two volt equal potential line, no
work will be needed.
4. If the person stood with the
side facing the tree, the feet would be at difference
potentials and a dangerous shock could be the result. If the
field around the tree is
uniform, then facing or your back to the tree would place both
feet on an equal
potential line and result in no shock. Facing away from the tree
would probably be
the preferable option because the face would be protected from
flying debris and
the flash of light.
Note: This experiment is not
an electrostatic experiment. As electric current passes
through the salt water, an IR drop is established and you are
using the voltmeter to
measure this IR drop. As you move the probe, keeping the readings
on the
voltmeter constant, you will be moving along regions of constant
IR drop.
Therefore, you will be identifying lines of constant potential
difference. In this
electric current situation, lines of constant potential difference
correspond to
equipotentials in the region surrounding the charges in an electrostatic
situation.
Experiment # 2-
Purpose:
To show the electric field around
a simple charge configuration and to relate these electric lines
to the equipotential lines in the previous experiment.
Materials:
This experiment uses
the same equipment as Experiment #1 on plotting equipotentials
except that the probe will now be in two contacts held a fixed
distance apart. This can be accomplished with nails through a
small piece of wood or plastic (clear plastic will give a better
view). A separation between the nails of about 3 cm usually works
well.
Procedure and Notes:
Wire the apparatus exactly as
in Experiment #1 except that this time the voltmeter will not
be attached to the "-" electrode, instead it will be
across the double probe . Place the double probe in the salt
water somewhere between the electrodes. Notice that, when you
rotate the double probe, there will be a particular orientation
which will give a maximum reading on the voltmeter. In this position
the line between the two probes will indicate the direction of
the electric field. If you start near the negative electrode,
rotate the double probe until you find the maximum reading. Then
move it so that the first nail is now in the position of the
second nail and again rotate to find the maximum reading. This
process will map out the electric field between the two electrodes.
Repeating this procedure with the map in another position will
result in plotting out another field line. After you have plotted
several field lines, compare these results with those of Experiment
#1 and notice that the
equipotentials are always perpendicular to the electric field
lines.
The apparatus is to be connected
to map out the electric field lines in the region between the
two electrodes. Rotating the double probe to give a maximum voltage
reading will indicate the direction of the electric field.
1. Give specific values in volts of changes in electric potential
in the tray.
2. Explain what is meant by the
term, "Electric Field Lines".
When you move along an
equipotential with a test charge, you will do no work. In an
external electric field this would be possible only if the charge
were moved perpendicular to the field. By the same token, if
you move in a direction of maximum potential difference, you
will be moving along a electric field line and you do work. Rotating
the double probe until the voltage across it is maximum results
in finding the maximum potential change and, consequently, the
direction of the electric field.
NOTE: This experiment is not
an electrostatic experiment. As electric current
passes through the salt water, an IR drop is established and
you are using the volunteer to measure this IR drop.


