P201 Menu
Exploratories
Electric
Forces & Fields
Terms to define
electric field -
the alteration of the properties
of space around a charged body that will affect a
test charge with a force, F. The closer the test charge
is to the body, the greater the force. The direction of the net
electric field is defined to be in the direction of the force
acting on a positive test charge. The strength of the force acting
on the test charge at each point in space is the magnitude of
the test charge times the electric field strength. Figure 1(a)
illustrates the electric field in the region of a pair of unlike
charges and Figure 1(b) illustrates the electric field in the
region of a pair of like charges.
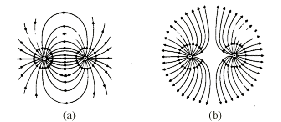
Figure 1
lines of force -
imaginary lines used in visualizing
fields such as electric fields. The lines
emanate from positive charges and terminate on negative charges.
The density of the lines in a region indicates the strength of
the field there.
SUPPORTIVE BACKGROUND
INFORMATION -
An historical look into the eighteenth
and mid-nineteenth centuries allows us to glimpse the beginning
of James Clerk Maxwell's electromagnetic wave theory. Coulomb
(1738 - 1806) had provided direct experimental evidence that
the inverse square law held true for electric charges and the
fields surrounding them.
Priestly had proposed this even earlier when he predicted that
electrical forces should behave in a way similar to gravitational
force. However, it took the experimental genius of Michael Faraday
(1791 - 1867) to introduce the concept of the electric field
and, thereby, to provide a qualitative description of the behavior
of electric forces.
Faraday was basically self-taught
with little formal education. Nonetheless he became a remarkable
chemist before turning his abilities as an experimentalist to
physics. Although Faraday understood little mathematics, this
did not inhibit his powerful insight which yielded qualitative
descriptions of the electrical field and electric forces. Scientists
like Gauss and Maxwell would eventually give a mathematical explanation
of Faraday's experimental description of the electric
field. After observing how iron filings arrange themselves around
a bar magnet, Faraday called the curved paths of the filings
lines of force. He visualized a similar pattern of lines around
positively and negatively charged bodies. Just as the lines appeared
to originate on one pole of the magnet and terminate on the other,
so he imagined that the lines of force of an electrical field
would originate on a positive charge and end on a negative charge.
Are Faraday's lines of force real? Faraday believed that physical
lines of force actually existed everywhere in space; today we
no longer believe that this is true. However, Faraday's visualization
of lines of force offers a model for understanding the electric
field and has provided the foundation for a quantitative explanation
of the phenomenon.
To define the electric field in mathematical terms, imagine a
single point charge q in space. When this is the only
charge present, there is no force acting on it. But let's imagine
a small positive charge q0, called a test charge, placed at a distance
r from q. Now both q and q0
experience the Coulomb force
F =
K e q q 0 / r
2 r
(Note: r is a dimensionless
unit vector in the direction of r .)
Regrouping the equation yields:
F =
q 0
(K e
q / r 2 r)
The quantity in the parentheses
does not depend on the magnitude of the test charge, but only
on its distance from q. The test charge detects the force,
but the quantity in brackets exist whether or not q 0
is there to detect it. That quantity is denoted by E and
is called the electric field generated by an isolated point charge
q.
E =
K e q / r 2
r
Electric Fields and
Potentials
1. An electric field
surrounds an electric charge. The field strength at any place
in the field can be found by placing a small positive test charge
there. Where the force on the test charge is great, the field
strength is great. Electric field strength is directly proportional
to the force exerted on a positive test charge. The direction
of an electric field at any point is the same as the direction
of the force
exerted on the positive test charge. Some electric field lines
surrounding a positive charge are shown.
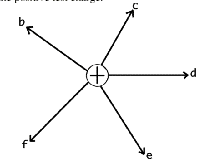
They extend radially from the
charge. A vector is sketched at point a to represent the
force that would be exerted on a positive test charge there (its
direction shows that like charges repel). Other points b,c,d,e
and f, are all located at the same distance from the
positive charge.
Draw a vector at each point b
- f to show the force on the same test charge.
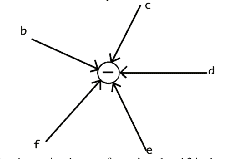
2. The electric field about a negative charge is shown to the
right. The field lines point radially inward, in the same direction
a positive test charge would be forced. Assume the magnitude
of the negative charge is the same as the charge above.
Draw field vectors at each of
the points h - m.
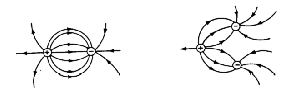
3. The pair of equal and opposite charges of questions 1 and
2 is shown below. Their individual fields, drawn uninfluenced
by each other, over lap to form a field pattern that can be constructed
by vector rules. This is shown at locations a and b,
where the two forces combine to a single resultant force. Note
that point b overlaps point m, and also points
c and l overlap. Note how the size of each vector
depends on its distance from the charge (inverse-square law).
Every point in the field is the result of both the positive and
the negative charges.
a. By vector rules, show the
resultant of all the vector pairs shown.
b. Sketch in sample vector resultants
at a few other places. Does the pattern that emerges agree with
the field pattern shown in Figure a on the next page?
4. Three points, (a,b,c)
are indicated on each electric field pattern. Point a in each
pattern shows the electric field vector at that point. The vector
indicates the magnitude and direction of the force that a positive
test charge would experience at that point (a curved field indicates
that the force on a nearby test charge would be different in
magnitude and direction). Use the vector at points a as
a reference and sketch in the electric field vectors for points
b and c in each pattern, using colored ink or pencil.


Electric Force & Fields
Everyday Connections
Early scientists initiated the intuitive view of a force
being a push or a pull. How can electric charges exert such pushes
and pulls without coming in contact with each other? In fact,
how does one charge "know" that another is around?
The question of pushes and pulls without actual contact centers
on the idea of "action at a distance", a concept that
bothered even Isaac Newton in his description of universal gravitation.
Michael Faraday first proposed the notion that a charge alters
the space around itself and creates a force field.
After viewing the three-dimensional patterns of lines of force
presented in the video, try sketching below some patterns yourself
in two dimensions.
What is the difference between the electric charge on an object
and the associated electric field?
An electric field does not deal with the body itself, but
the region surrounding it. It describes the alteration of the
space in the region surrounding the body and results in an electric
force detected by a test charge entering the region. In other
words, the charge is the "thing" that causes the field.
An analogy might be the difference between a rose and the pleasant
fragrance which surrounds it.
Why do electric lines of force never cross?
The electric field E has a unique direction at any
point in space. If two lines crossed, two directions would be
indicated for E at the point of intersection and the electric
field would not be unique at that point.
How do charges distribute themselves on the surface of
a spherical conductor under electrostatic conditions?





