This Is Work

This Is Work!

Problem:

What is work?

Procedure:

1. Pick a distance of a meter or so. Sense how much effort it takes to push a heavy book along the horizontal that distance. How much more effort does it take to push it twice as far, or twice or fast?
2. Place a similar book on top of the original one and sense how much effort it takes to push the two books through the distance you picked.

Summing Up:

1. From your study of sliding friction, what is the relationship between the mass of a sliding object and the friction force it experiences?
2. On the basis of your experience with sliding friction, estimate how much more force you have to apply to push two books compared to one book.
3. If the "effort" it takes to move an object is associated with physical work, guess an equation that can be used to define work mathematically when the force on an object and its displacement (i.e., the distance it moves) lie along the same line.

Pulling at an Angle- What Happens When the Force and the Displacement Are Not Along the Same Line?

Let's be more quantitative about measuring force and distance and calculating the work. How should work be calculated when the external force and the displacement of an object are not in the same direction? For this project you'll need:

· A 0-5 N spring scale
· A fairly smooth horizontal surface
· A wood block with hooks in it
· A set of KG weights

A block sliding on a one-dimensional surface. Before you make your simple force measurements, you should put some weights on your block so that it slides along a smooth surface at a constant velocity even when it is being pulled with a force that is 45 degrees from the horizontal.

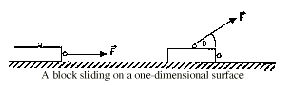
Activity: Calculating Work

(a) Hold the spring scale horizontal to the table and use it to pull the block a distance of 0.5 meters along the horizontal surface in such a way that the block moves at a constant speed. Record the force in newtons and the distance in meters in the space below and calculate the work done on the block in joules. (Note that there is a special unit for work--the joule or J for short. One joule is equal to one newton times one meter, i.e. J = N·m)

(b) Repeat the measurement, only this time pull on the block at a 450 angle with respect to the horizontal. Pull the block at the same speed. Is the force needed larger or smaller than you measured in part (a)?

(c) Assuming that the actual physical work done in part (b) is the same as the physical work done in part (a) above, how could you enhance the mathematical definition of work so that the forces measured in part (b) could be used to calculate the work? In other words, use your data to postulate a mathematical equation that relates the physical work, W, to the magnitude of the applied force, F, the magnitude of the displacement, d, and the angle, , between F and d Explain your reasoning.

Hint:

sin 300 = .500, ... sin 450 = .707, ... cos 300 = .865, ... cos 450 = .707.