P201 Menu
Exploratories
How Hot Are Your Hot Wheels™?
Problem:
How can you apply the conservation of energy concept to 1)
predict from where to
release a car on a loop-the-loop track to just retain contact
with the track through the loop and 2) predict how far and how
high a car will travel from a ramp inclined at some angle?
Materials:
Hot Wheels™ set with loop-the-loop and ramp, small
car, meter stick, timing device (Computer interface photogates,
if possible).
Procedure A: Loss of Energy Due to Friction
The illustration shows the track setup for Procedure A. Elevate
both ends of the track to a height of about 1m above the floor
or lab table.
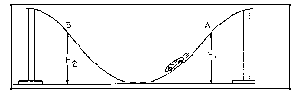
Release the car from the starting point A. Record this height
(h1) and the height to which the car rises (h2)
on the other end of the track. Please make several trials. It
is important to secure the track to the floor so some of the
car's energy is not transformed into motion of the track.
The ratio of the final height to the initial height is equal
to the ratio of potential energy transferred back into the car
going up the left ramp to the potential energy the car had at
the top of the right ramp at point A. Call this ratio of h2
to h1 the "efficiency" of the system for the
car going from point A to point B on the track. The distance
along the track from A to B is called the "standard length"
so the ratio of h2 to h1 (efficiency) represents
the fraction of the initial energy the car will have when it
reaches point B on the track. This ratio is used in later experiments
to determine how high the car must start, so it will have a predictable
total amount of energy when it reaches certain points on the
track.
Summing Up:
1. What is the average height ratio, or efficiency?
2. In what unit is efficiency measured?
Procedure B: Loop the Loop
The next illustration shows a loop-the-loop section placed
in the track at about the
standard length from the starting end of the track. The problem
is to predict the minimum height from which the car must start,
so it will successfully travel all the way around the loop without
falling away from the track. In order for this to take place,
there must be centripetal force acting on the car as it goes
around the loop. This force Fc must be equal to the weight
of the car.
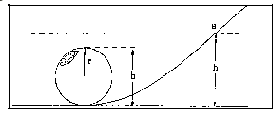
The equations for centripetal force and weight appear below.
W = F 0
....W = mg .... F 0
= mv 2
/ r
Combine these equations and solve for v 2
What is the minimum speed the car can have at the top of the
loop to perform a
successful loop?
At the top of the loop, the car has both kinetic and potential
energy. This energy total was supplied by the loss of potential
energy the car had at a point a. This means:
KE b + PE b
= PE a
or
1/2mv 2
+ 2 mgr = mgh
Substitute the value of v 2
you found above into the kinetic energy equation and then solve
the total energy equation for h. this means that if there
were no friction, the car should start from a height, h, to
make it around the loop. Since the system does have friction,
the car must start from a point just higher to make up for the
frictional loss. Therefore the car must start from a height of
h divided by the efficiency of the system. Write a report
on your findings in this experiment.
Summing Up:
1. State in your own words the energy changes as you lift
the car to point A, until it
completes the loop-the-loop.
2. Do your results show that energy is conserved? Explain your
answer.
Procedure C: The Dare Devil Jump (Optional)
The illustration below shows the jump-ramp set up. The problem
here is to calculate the range of the car's jump when you release
it from a chosen height (h) above the launch point of
the ramp.
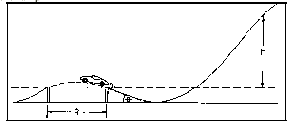
The starting point of the jump should be at the "standard
length" from the release point of the car. The kinetic energy
of the car at the launch point on the ramp equals the loss in
gravitational potential energy from the starting point on the
track, or
1/2 m v 2
= mgh,
assuming the track is 100% efficient. From this statement
of conservation of energy, you can begin to solve the problem
posed above. Calculate the loss in gravitational potential energy
your car would undergo from the release point to the top of the
launch ramp. Now calculate the actual energy at launch by using
the efficiency factor you calculated in Procedure A. From this
kinetic energy, you can calculate the launch velocity of the
car.
You can calculate or measure the initial launch angle of the
car, and use this to calculate the vertical and horizontal components
of the launch velocity. From your knowledge of projectile motion,
you should now be able to calculate the total jump time and the
jump range. Now try out your predictions! How did you do? If
time permits calculate the maximum height of a "fence"
the car could clear as it jumps from ramp to ramp.
Summing Up:
1. Describe the energy changes as a car moves down the track
and completes the jump.
2. Explain whether or not energy was conserved in this activity.
Teacher Notes
Teaching Strategies:
The principle of conservation of energy is one of the most
powerful and widely used concepts in solving science related
problems. This activity is an example of the type of problem
frequently found as an end-of-chapter numerical exercise. Students
should find this type of application more interesting than the
usual end-of- chapter exercise. Whereas textbook problems often
neglect friction in word problems, students deal with it here
in a practical way and apply it to make predictions of motion
of the Hot Wheels™ car.
The mathematics in Procedure C is challenging. You may wish
to make Procedure C optional, or provide extra help for struggling
students.
If you do not have a Hot Wheels™ set in your school,
it is well worth asking students to bring in enough Hot Wheels™
sets so you have at least one for every two to three students.
For most predictable results secure the track, loop-the-loop
and ramp with clamps or tape.
Sample Observations/Calculations Procedure A:
h 1
= 40cm h 2
= 32cm
eff = 32 cm / 40 cm = 0.80 = 80%
Summing Up Procedure A:
1. Friction reduces the effect of useful work and basically
drains off some of the energy intoa heating effect. To compare
the initial height, h 1,
of the car with the final height, h 2
,is to compare the initial potential energy of the car with its
potential energy on the other side of the track (because m
and g are constant). An efficiency of 80% means that
80% of the initial potential energy at h 1 transfers to potential energy
at h 2 or
that 20% of the initial potential energy was lost to frictional
forces. This efficiency applies only to the "standard length"
of track. For a longer track, the difference in elevations would
be greater.
2. Efficiency is a ratio, so it has no units. The units always
divide out.
Sample Observations/Calculations Procedure B:
1. They should take several sets of data, calculate the efficiency
for each set, and then calculate the average efficiency. Students
will use this average in Procedures B and C.
2. Efficiency is a ratio, so the units have divided out. Since
the weight of the car will be equal to the centripetal force
at the top of the loop we can write
W = F c
But
W = mg, .... and F c
= mv 2 / r
So
mg = mv 2
/ r
v 2
= gr
Typical values might be:
d = 20 cm, r = 10 cm, and
v 2
= 9.8 m/s/s * 0.10m = 1.0 m/s
Summing Up Procedure B:
In the equation, v 2
= gr , v ...is the minimum speed of the car at
the top of the loop for the wheels to just touch the tracks.
If the energy is conserved in this event, then the potential
energy at A should equal the sum of all the energies at some
other point such as at the top of the loop. In the form of an
equation, we write
PE a =
KE b
+ PE b
+ E friction
Recognizing that we will adjust for the energy lost to frictional
forces in our release height we have by substitution:
mgh a
=1/2 mv 2
+ mgh b
or
gh a
= 1/2 g r + g (2r) .....where v 2 = g r ...
and
h b
= 2 r .... and h a
= 1/2 r + 2 r = 2.5 r
As pointed out in the student sheet, we must now concern ourselves
with the effect of frictional loss. Measuring our "standard
length" from B back to A we should elevate point A such
that its height h is found as:
0.80 h = 2.5 r .... or ... h = 3.125
r
Note that the mass of the car does not affect the height from
where it should start. Check to determine that all forms of energy
are accounted for in the conservation equation. The KE B term represents
linear kinetic energy so if you use a steel ball instead of a
car then some of the energy transforms into rotational energy,
which for a solid sphere would be mv 2
/5. . Add this term to the other terms in equation 2 and
3. In applying equation 2 and 3 to the car we will assume that
the wheels take on a negligible amount of rotational kinetic
energy.
1. When the car is lifted, work is done on it, increasing its
potential energy. The
work done to lift it to point A equals its potential energy at
point A. As the car is
released, it rolls down the ramp, losing some of its potential
energy, but gaining in
kinetic energy. The loss in potential should equal the gain in
kinetic. At the
bottom, the potential is zero, but the kinetic should be equal
to what the potential
was at point A. As the car enters the loop-the-loop, it loses
kinetic energy but
gains potential. The opposite happens on the way down. At any
point, the total
energy should equal the work done in lifting the car to point
A.
2. ... m = 30 g = 0.03 kg
At point A PE = mgh = ( 0.03 kg ) ( 9.8 m/s/s )( 0.31
m ) = 0.091 J
At top of loop KE = 1/2mv 2
= ( 0.5 ) ( 0.03 kg ) ( 1.0 m/s )2
= .015 J
PE = mgh = . ( 0.03 kg ) ( 9.8 m/s/s ) ( 0.2 m ) = .059
J
KE . and PE = 0.015 J + 0.059 = 0.074 J
Energy lost = 0.091 - 0.074 = 0.017 J
Energy lost went into heat produced by friction.
Sample Observations/Calculations Procedure C:
These sample calculations use a release height ,h, of
.40 m above the launch point and a track efficiency of 80%. The
launch angle is 30 0 and mass of the car is .03 kg. Gravitational
potential energy = mgh = ( .03 kg ) ( 9.8 m/s/s ) ( .40 m ) =
.12 J. Actual kinetic energy = efficiency x potential energy
= (.80)(.12 J) = .094 J.
Because kinetic energy =1/2mv 2
. then v 2
= 2 * KE/m . or
v 2
= (2) (.094 J) / (.03 kg) = 6.3 m 2
/ s 2 or
v . = 2.5 m/s.
The vertical component (vy
) of launch speed is used to calculate the time the
car spends in the air after launch. V y = v sin .q
= ( 2.5 m/s ) ( 0.5 ) = 1.25 m/s. Calculate the time in the air
from the definition of acceleration, or t = v/a assuming
the vertical velocity at the peak is zero. Then the time for
one-half of the flight = 1.25 m/s 9.8 m/s/s = .13 s, or the total
time of the flight is .26 s. Calculate the range by first finding
the horizontal component (v h) of the launch
velocity, v h
= V cos .q = (2.5 m/s)(.866)
= 2.2 m/s. This horizontal velocity component is constant and
not affected by gravity. Therefore the range is simply the product
of the total time in the air and the horizontal velocity. Range
= ( 0.26 s ) ( 2.2 m/s ) = 0.56 m.
Summing Up Procedure C:
1. Answers could be very similar to Procedure B, #1.
2. Within experimental error, energy is conserved. Work was done
in lifting in the car. From that point on, no more work was done
on the car (except friction) to change the total energy.


