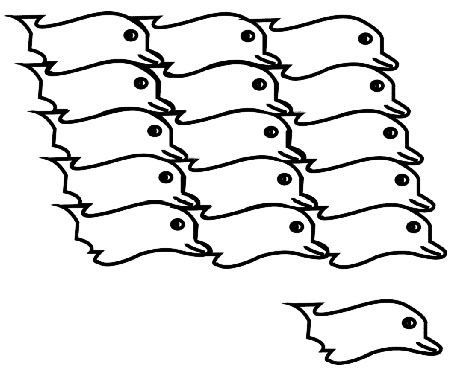
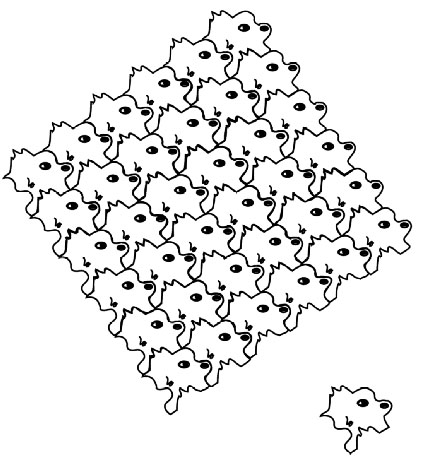
The dolphin pattern is the result of a rectangle. The dog is from a square.
3. Once you have created a new pattern use graph paper and glue the pattern to card stock for ease in drawing your Escher-type pattern.
Terrific Tessellations
Problems: What is the basis for symmetry? How can a complex pattern be generated from a simplistic geometric shape?
Materials:
Graph paper, scissors, card stock.
Procedure A:
1. Choose a geometric shape that will tile, i.e., square, rectangle, equilateral triangle or a hexagon.
2. Create a "new" pattern by removing a section from one side of the geometric shape and adding it to the opposite side with rectangles, squares or hexagons or to the neighboring side as in hexagons or triangles.
Examples:
The dolphin pattern is the result of a rectangle. The dog is from a square.
3. Once you have created a new pattern use graph paper and glue the pattern to card stock for ease in drawing your Escher-type pattern.
Procedure B:
Make your name in such a fashion that it obeys dot symmetry. This means that if a dot were placed in the middle of your name and you rotated your name 180 degrees, it would look the same.
See the examples of JESSIE and JON:
Summing Up:
1. In each of these cases what is the symmetry involved?
2. How do these tessellation's correspond to fractal patterns?
3. Where do you find fractals or Chaotic Crystals in nature?