Ball_Bounce

Student Design of Drop Bounce Experiment

The day before the experiment the students should be placed in groups according to their learning styles. They should be given the following assignment and given some time in class (if possible) to work on it. This lab can be used as a culminating activity for the unit Habits of the Mind. The Drop Bounce Lab addresses all of the learning objectives from Working With Others to Explains Results. If the experiment is performed near a concrete block or brick wall students can estimate the distances to the nearest 1/4 of a block. The experiment could be done just as easily with meter sticks. Either approach leads to the discussion about estimation.

Student Homework Assignment:

Problem:

What is the relationship between the height from which a ball is dropped and the height to which it bounces?

Procedure:

You are to design a lab experiment to answer this question. You should consider the following as you design your lab:

What equipment will you need?

What data do you need to collect?

What variables must be measured? Which variable(s) do you control?

Set up a data table to help in organizing your thoughts and data collection.

Teacher Discussion Before Drop Bounce Lab:

The morning after the homework assignment where the students design their labs, the teacher should look over the designs quickly and allow for some discussion. The primary emphasis of the teacher discussion should be about estimation. Emphasis should be placed on the fact that ALL measurements involve making estimations no matter how accurate the instrument. Comparison could be made between estimating the distances to the nearest quarter of a concrete block to estimating to the nearest centimeter on a meter stick.

Once the experimental design has been approved, students will perform the experiment measuring the height from which the ball is dropped and the height to which the ball bounces and graph the data.

A copy of a pre-designed lab is attached in case there is not enough time during the first few days to allow for student-designed labs

Student Discussion of Drop Bounce Lab:

The students should be allowed some time within their groups to get the data into table form, graph the data and discuss what it means. They can compare their graph with the graphs from other groups.

Drop Bounce Lab

Problem:

What is the relationship between the height from which a ball is dropped and the height to which it bounces?

Materials:

"Superball" or other balls, wall made of cinder blocks or bricks, (meter stick - optional)

Procedure:

1. The experiment should be done near a cinder block (or brick) wall so that the distances can be estimated to the nearest fourth (1/4, 1/2, 3/4, 1) of a cinder block. Some time should be spent in the beginning to practice estimating distances this way.

2. Divide the activities so that one student drops the ball, one student watches the bounce and estimates the height to which it bounces, and one student records the data.

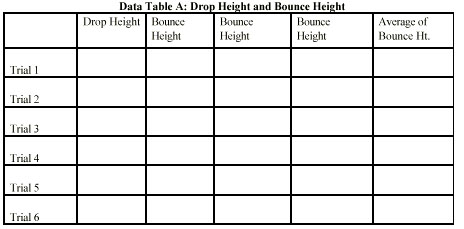
3. Drop a superball from various heights. The height to which the ball bounces is to be estimated as carefully as possible. Both the height of drop and the height of bounce should be recorded in data table A.

4. Drop the ball at least two times from each height with the average of the bounce heights used asthe final measurement. If there is too much variation in these two measurements, take a third measurement.

5. Drop the ball from at least six different heights beginning at about two blocks. Increase the height of drop by at least one block at a time until six or more drops have been completed.

6. Care must be taken in doing the estimations. Drop the ball from the line between cinder blocks/bricks to make the measurements more accurate. Use the same point on the ball (top) or (bottom) when judging both the height of the drop and the height of the bounce.

7. Draw a graph of bounce height Vs drop height.

8. Draw a best fit line for the data points. Note: This is NOT a line drawn to connect each point. It is a line which best shows the relationship involved - in this case a straight line.

9. Compute the slope of the best fit line. Note: This is NOT the slope between the first and last data points.

10. Write the equation for the graph using the slope-intercept form ( y = mx + b ). The line of the graph may not go through the origin as the bottom cinder block may be elevated above the floor.

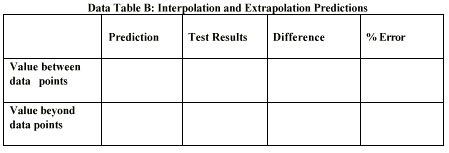
11. Use the graph to predict the height of the bounce for a ball dropped half way between two drop heights. This is called interpolation. Record your prediction in data table B.

12. Use your graph to predict the height of the bounce for a ball dropped from twenty or thirty bricks high. This is called extrapolation. Record your prediction in data table B.

13. Test the predictions by dropping the ball from the chosen heights and measuring the bounce. Compare your predictions with the results from testing. Check with other groups and see if their results are similar to yours.

Summing Up:

1. Were your measurements that you took during the lab precise? Were they accurate? What's the difference? Describe how your measurements were or were not precise or accurate.

2. After reading over the information on sources of error from handout H012, identify all sources of error for the Drop Bounce Lab. List each and label it as one of the three types of error given in the handout. Then explain how each of the sources of error in the lab could be minimized

3. Identify the dependent and independent variables in this lab. Explain what the rule is for graphing independent versus dependent variables.

4. What happens to the bounce height as the drop height increases? What relationship does this suggest?

5. Calculate the bounce height for a 3.5 meter drop. First convert your units of brick/blocks to meters. (Show your conversion process)

6. How does your answer for the above compare with that of other groups? Is it larger, smaller the same?

7. If there is a difference, explain in detail what you believe accounts for the difference.

8. After you graphed your data you were asked to interpolate and extrapolate information from your graph. What do you conclude about the accuracy of information found from a graph by interpolating between data points and extrapolating beyond them? Explain your answer.